2019. február 26.
A nem-egyensúlyi termodinamika matematikai és kísérleti módszereinek fejlesztésére kaptak jelentős támogatást a GPK kutatói.
„A mérnöki tervezésnél nemcsak egy adott anyag statikus tulajdonságai lényegesek, hanem az is, hogy ezek az időbeli, dinamikus folyamatokban hogyan játszanak szerepet. Az anyagokat jellemző paraméterek egy részét ma már régóta ismerjük: kutatásainkban a hangsúly inkább ezek pontosításán, valamint új paraméterek megismerésén van – hangsúlyozta a bme.hu kérdésére Kovács Róbert, a BME GPK Energetikai Gépek és Rendszerek Tanszék adjunktusa, akinek kutatócsoportja „A nem-egyensúlyi termodinamika matematikai és kísérleti módszereinek fejlesztése” című projektjére a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFIH) pályázatán nagymértékű támogatást kapott. A szakember kifejtette: „az építésre használt kőzetek esetében például a különféle időjárási hatások által előidézett hőmérsékleti ingadozások lehetnek fontos tényezők, de a legtöbb heterogén szerkezetű alkatrésznél, – például a kompozitanyagokból gyártottaknál –, amelyeknél a működési körülményektől függően meglehetősen gyorsan változik a hőmérséklet, fontos, hogy tudjuk ezt az időbeli viselkedést előre jelezni és tervezhetővé tenni. Ennek az a jelentősége, hogy így az adott alkatrész biztonságos üzemi feltételek mellett használható, illetve az élettartama növelhető, esetleg a terhelhetősége jobban kihasználható. Vannak olyan időintervallumok, amikor a klasszikus, jól bevált modellek nem működnek: mi ezeket próbáljuk meg feltérképezni”.

|
Az NKFI Hivatal 2018-ban meghirdetett „Jelentős nemzetközi hatású, kiemelkedő eredményeket elért kutatócsoportok támogatása” (KH_18) című, / /1,2 milliárd forint keretösszegű pályázati felhívásával arra ösztönzi a hazai kutatócsoportokat, hogy újabb, szakterületük fejlődésére nagy hatást gyakorló, további kutatásokat, illetve alkalmazott fejlesztéseket megalapozó eredményeket érjenek el, és azokat a legnagyobb láthatóságot jelentő nemzetközi tudományos folyóiratokban ismertessék, jelentős idézettséget elérve. A 2. értékelési szakaszra jelentkező hazai kutatócsoportok pályázatai közül 32 felelt meg a szigorú feltételeknek és nyert összesen csaknem 616 millió forint támogatást a hazai tudományos eredmények nemzetközi láthatóságát ösztönző kiválósági programban. A műegyetemi szakemberek közül ezúttal Kovács Róbert, valamint Pukánszky Béla, a Vegyészmérnöki és Biomérnöki Kar (VBK) Fizikai Kémia és Anyagtudományi Tanszék egyetemi tanára által vezetett kutatócsoport nyert. „A nem-egyensúlyi termodinamika matematikai és kísérleti módszereinek fejlesztése” című, 2018 decemberében indult kétéves projekt tagjai Gróf Gyula egyetemi docens, az Energetikai Gépek és Rendszerek Tanszék vezetője, Kovács Róbert adjunktus témavezető, másrészt fiatal szakemberek: Szűcs Mátyás, Rieth Ágnes, Fodor Tamás, Balassa Gábor. A kutatások Ván Péter, az Energetikai Gépek és Rendszerek Tanszék tudományos munkatársa, valamint Fülöp Tamás adjunktus korábbi munkájára épülnek. |
Kovács Róbert a témával már egyetemi hallgató korában megismerkedett. Géptervező alapképzésének megszerzése után a gépészeti modellezés mesterszakot a BME-n végezte, ahol találkozott későbbi témavezetőjével és mentorával, Ván Péterrel. A közös munkának meglett a gyümölcse: a hallgató kutatásai idővel TDK pályázatot, diplomamunkát, majd doktori értekezést eredményeztek.
A nyertes kutatócsoport munkájának kísérleti oldala sajátos vizsgálatok sorozatára épül. Egy speciális műszerrel mintákat – például kis, korong alakú csiszolt kőzetet – felvillanó fénnyel sugároznak be, majd mérik a minta hőmérsékletváltozását és abból következtetnek az anyag viselkedésére. „A feladatot inhomogén szerkezetű anyagokkal végezzük: például kőzetekkel, amelyekben vékony repedések lehetnek, vagy fémhabokkal, amelyekben gázzárványok vannak. Munkánkat a továbbiakban minden anyagtípusra szeretnénk kiterjeszteni. Efféle kutatásokat már régen is végeztek, de az elméleti interpretáció hiányában nagy részük elakadt. Remélhetőleg a jövőben előrelépünk e területen” – bizakodott a kutató, hozzáfűzve, hogy a szakirodalomban jegyzett, de általuk el nem érhető, nagyon alacsony hőmérsékleten lebonyolított kísérletek eredményeinek megismerésére és elemzésére is törekednek.

Flashmérő modell
A mérések során olyan jelenséget vizsgálnak, amely nevére még nincs egyértelmű magyar szakirodalmi kifejezés, egyfajta túlcsillapított (over-diffusive) hővezetésnek lehet nevezni, ami a mérési diagramon is megfigyelhető. „Ez az, ami más időbeli viselkedést jelent egy adott időintervallumban a klasszikus, Fourier-egyenletre épülő modell előrejelzéséhez képest. Ennek van egy megfelelő módon kiegészített módszertana, a nem-egyensúlyi termodinamika, amelynek révén lehet elméleti úton megmagyarázni az említett jelenségeket” – hangsúlyozta Kovács Róbert, egyúttal említve az okot, amiért a több párhuzamos hővezetési mechanizmussal egyszerre rendelkező inhomogén szerkezetű anyagok vizsgálatába belefogtak.
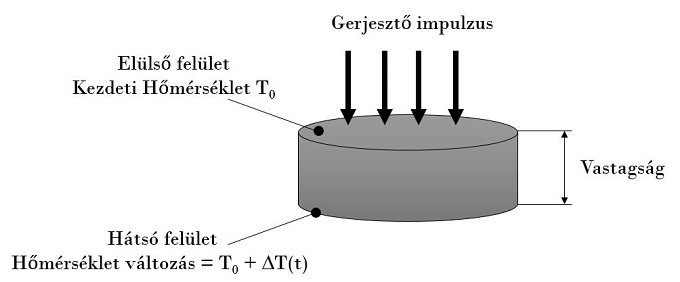
Flashmérés (sematikus ábra)
„Az első vizsgált minta, amelyen ezt a jelenséget sikerült kimutatnunk egy kondenzátorból kivágott, réteges szerkezetű darab volt: e rétegeket jó és rossz hővezető képességű részek párhuzamosan alkotják, de a kőzetek vagy a fémhabok is ezzel analóg módon épülnek fel: vannak jobb és rosszabb vezetőképességű részeik. A felhasznált elméletben azonban az a szép, hogy nincs benne megkötés az anyagtípusra: egyaránt leírhatjuk vele a kövek, a kompozitok, de akár szerves minták, például a bőr vagy a hús viselkedéseit is” – ecsetelte a kutató. A lézeres műtéti beavatkozásoknál például nagyon hasznos lehet, ha meg tudjuk jósolni a szövetekben kialakuló hőmérsékletet, mert egy adott idő elteltével már az egy-két fokos eltérések is égési sérüléseket okozhatnak.

Fémhab és nagyítása

Kondenzátor és nagyítása

Szürke középszemcsés homokkő és nagyítása
„A projekt célja, hogy a már meglévő termodinamikai elméleti modelleknek a gyakorlatba való átültetését javítsuk. Például új numerikus módszereket vagy analitikus megoldásokat keresünk, lehetővé téve egy már kidolgozott elméleti háttér esetében konkrét egyenlet, összefüggés biztosítását egy ismert mérnöki probléma kiküszöböléséhez. Kihívást jelent, hogy részben alapkutatásról van szó, tehát olyan jelenségekkel foglalkozunk (pl. összetett, mérnöki berendezésekben megjelenő alakzatok esetén), amelyeket más még nem dolgozott ki, egy-egy gépészeti berendezésre, alkatrészre ezeket az egyenleteket még nem vázolták föl.
A szimulációk során fel kell használni egy geometriát, ami ha összetett, akkor csak valamilyen kifejezetten ilyen célra kidolgozott programmal lehet kezelni. Másfelől, egy-egy modell tulajdonságait csak nagyon leegyszerűsített geometrián, például egy vonal elemen megoldva lehet tanulmányozni és megérteni. Nincs még egységes, rögzített háttere a területnek, mint az alkalmazott tudományok többségének. A módszertant, tehát hogy miképpen használjuk és értelmezzük elméleti tudásunkat, valamint milyen matematikai eszközökre van szükség ismereteink gyakorlati alkalmazásához, az alapjaitól kell felépíteni és ennek megvannak a maga fizikai, matematikai kihívásai” – vallja a fiatal szakember. Hozzátette: a másik kihívás, hogy olyan ipari alkalmazást találjanak, ahová azonnal átültethetők az eredmények és amely így jól látható, kézzelfogható előnyökkel jár. „Ez azért nehéz, mert gyakran körülményes hozzáférni az ipari adatokhoz, kutatásokhoz, például mikroelektronikában: pedig kutatásaink a mikroprocesszorok, vagy általában a nanotechnológiában használatos anyagok termikus viselkedésére jobb modellt fognak adni, amely a korábbinál pontosabb leírását adja az inhomogén anyagoknak” – ecsetelte a kutató.
A hasznosítási területek szerteágazóak lehetnek: a gépészeti tervezésnél bárhol, ahol heterogén anyagokkal foglalkoznak; biomérnöki alkalmazásokban, ahol fontos a szövetek viselkedésének modellezése; energetikai alkalmazásokban, ahol fontos az erőművi vagy energiatárolásra alkalmas berendezések hatásfokának javítása, élettartama, kihasználtsága, illetve az űrtechnológiában használt anyagok (fémhabok) tervezésekor. „A vizsgálat várhatóan a kutatási támogatás lejárta után is folytatódik, így új forrásokra pályázunk majd” – árulta el a szakember.

A kutatók tevékenysége az oktatásban is hasznosul: a mérnökök számára új, modern szemléletet adhatnak át, valamint bemutathatják számukra a vizsgálatok eddig elért eredményeinek már meglévő modellekre gyakorolt következményeit is, amely tudást máshol nem kaphatnak meg.
„A kihívás számomra ebben az, hogy egy tisztán elméletiből valamilyen gyakorlati, kézzelfogható és széles körben felhasználható eredményt érjek el. Ebben a feladatban sokféle látásmód egyesítése szükséges: mérnöki, matematikai és fizikai egyszerre, amelyek összhangja együtt alkotja a kutatások szilárd alapjait. Mindehhez nélkülözhetetlen a kreativitás és egy nyitott, esetenként absztrakt szemlélet is” – összegezte Kovács Róbert, a kutatócsoport vezetője.
HA-GI
Fotó: Philip János