2020. június 18.
A több tudományterületen is hasznosítható újításukról neves nemzetközi folyóiratban publikáltak a szakemberek.
„A mérnöki tudományokban (a hullámterjedéses anyagvizsgálattól a klinikai MRI szkennerek beállításáig, az elektromos áramkörök tervezésétől a geológiai struktúrák feltérképezéséig) széles körben alkalmazzák a Laplace transzformációs eljárást. Az általunk kidolgozott számítási lehetőség kiküszöböli az eddigi Laplace transzformációs módszerek hibáit és minden eddigi módszernél megbízhatóbb eredményeket szolgáltat, ezért a 'világbajnoki címre' is esélyes” – tájékoztatta a bme.hu-t Telek Miklós, a BME Villamosmérnöki és Informatikai Kar (VIK) Hálózati Rendszerek és Szolgáltatások Tanszék egyetemi tanára, kutatócsoport-vezető, miután az MTA-BME Információs Rendszerek Modellezése kutatócsoport és a Tanszék kutatóinak tanulmánya megjelent a rangos Performance Evaluation szaklapban. A kutatócsapat (Horváth Gábor egyetemi tanár, Horváth Illés, Telek Miklós) olyan új, numerikus inverz Laplace transzformációs metódust dolgozott ki, amely két alapvető problémát old meg egyszerre: a Gibbs oszcillációt (“túllövés”, “alullövés”) és a numerikus stabilitást.
|
A numerikus eljárás egy, a csapat által művelt szélesebb kutatási terület, a tömegkiszolgálási rendszerekben hatékonyan alkalmazható mátrix-exponenciális eloszlás vizsgálatának eredménye. Az új módszer központi eleme a Dirac-delta függvény olyan, koncentrált mátrix-exponenciális (Concentrated Matrix Exponential, CME) sűrűségfüggvénnyel való közelítése, amely a nem-negatív értékkészlete miatt biztosítja az oszcilláció-mentességet. Az “aritmetikai zaj” hatása is nagyságrendekkel kisebb az új eljárásban. Ez azt is jelenti, hogy adott számábrázolási rendszerben az eddig ismert módszerekhez képest nagyságrenddel több ponton (tehát nagyobb pontossággal) lehet kiértékelni az inverz transzformációt. |
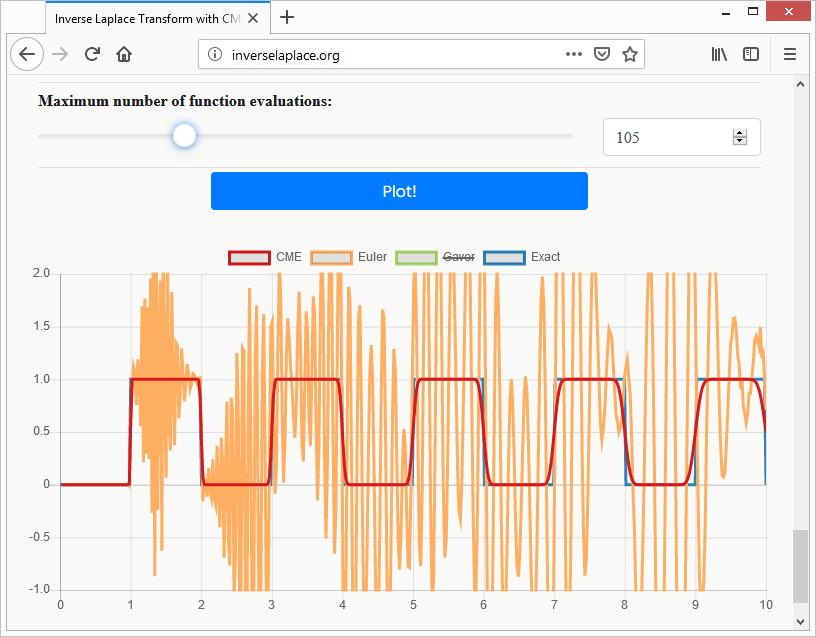
A négyszögfüggvény Laplace transzformáltjának numerikus inverz transzformációjával is a CME módszer bírkózik meg a legjobban. Az ábrán jól látható a CME oszcilláció- és gerjedésmentes viselkedése.
Gondoljunk csak bele, hogyan értékeljük az eddig ismert módszerek alkalmazásával kapott eredményeket abban az esetben, ha valamiféle csillapodó periodikus viselkedést tapasztalunk, vagy zajszerű jellel modulált függvények jelennek meg? Az ilyen hibás inverz transzformáción alapuló következtetések rendkívül félrevezetőek lehetnek, hiszen ezeket a jelenségeket a nemkívánatos Gibbs oszcilláció és az aritmetikai zaj is okozhatja. A CME módszer alkalmazásával ez nem fordulhat elő! – hívták fel a figyelmet a kutatók.
 :
:
A számítási módszerek pontatlanságát illusztráló grafika. Az eddig alkalmazott legjobb technikák (Euler, Gaver) nem adták vissza az eredeti „formát” (függvény alakot), a CME viszont igen.
Az új módszerről rövid angol nyelvű ismertető jelent meg és demó is készült.
– GI –