Mérnöki tudás egyaránt segíti a fertőzés terjedési dinamikájának jobb megértését. A kutatásban a BME külső munkatársa is részt vett.

„A járványügyi intézkedéseknél figyelni kell arra, hogy a túl szigorú megszorítások, habár hatékonyak a betegség terjedésének lassításában, negatív hatással vannak a társadalomra és a gazdaságra. Érdemes egyensúlyra törekedni, azaz olyan stratégiát keresni, amellyel a járvány kezelhető, miközben a beavatkozás mértéke elviselhető szinten marad. Kollégáimmal a sikeres folyamathoz fogalmaztuk meg a kritériumokat, matematikai eszközökkel modellezve a helyzetet” – világította meg a közelmúltban publikált tanulmányuk jelentőségét Péni Tamás, a BME Közlekedésmérnöki és Járműmérnöki Kar (KJK) Közlekedés- és Járműirányítási Tanszék külső munkatársa, a SZTAKI Rendszer és Irányításelméleti Kutatólaboratórium tudományos főmunkatársa. A kutatás a Nonlinear Dynamics folyóiratban olvasható a népszerű, feltörekvő kutatási területeket bemutató, Feature Article című új sorozat legelső cikkeként.

„Járványmodellezés és stratégiatervezés szempontjából meg kell különböztetni azt az esetet, amikor még nem áll rendelkezésre megfelelő oltóanyag, attól az esettől, amikor a vakcina már elérhető a társadalom számára. Az előbbi esetben kizárólag a kontaktusok korlátozása révén befolyásolható a járvány terjedése, az utóbbi esetben az optimális oltási stratégia kidolgozása a cél. Minden esetben folyamatosan mérlegelni kell a fertőzés terjedését korlátozó intézkedések gazdasági-társadalmi hatását, hogy a lépések semmiképpen ne vezessenek az egészségügyi rendszer összeomlásához, vagy pénzügyi válsághoz. A Röst Gergely vezetésével dolgozó szegedi matematikusok által megalkotott verzióban – amelyet a magyarországi helyzetre optimalizáltak – terveztünk egy szabályozást, egy irányítást, ami meghatározza, miképpen, milyen súlyú megszorítások alkalmazhatók fél éves távlatban az egyes hónapokban” – ismertette Péni Tamás, hozzátéve: a megalkotott modell számos paramétertől függ, ezek a járvány viselkedését, terjedését, a betegség lefolyását jellemzik, pl. lappangási idő vagy a terjedési sebesség. A paraméterekre a járványról világszerte gyűjtött adatok alapján tudnak becsléseket mondani; és habár ezek a rendelkezésre álló adatok számának növekedésével egyre pontosabbak, stratégiatervezés esetén a paraméterek bizonytalanságával mindig számolni kell.  

„A munka kezdetén nagyon sokat kellett tanulnunk, mert többségünk korábban sosem foglalkozott kifejezetten járványdinamikával: megismertük a szakterület speciális tulajdonságait és terminológiáját, amelyre az irányításelméletnek a mérnöki munkában egyes, rutinszerűen használt módszereit jól alkalmazhattuk” – emelte ki a szabályozáselméleti szakértő. A munka eredményeként létrejött a járvány terjedését leíró matematika modell. „Ez egy dinamikus rendszer, amelyben az állapotváltozók a betegség különböző fázisait jelentik, értékük az adott fázisban lévő betegek száma. Vannak az egészségesek, a már megfertőződöttek, a látensek, akik kapcsolatba kerültek a betegséggel, de nincsenek tüneteik, viszont tudunk róluk, és végül a panaszmentesség miatt előtérbe nem kerülő, ún. aszimptomatikus esetek. Ezt a láncolatot modellezi a dinamika: a járványhelyzet természetéből fakad, hogy nem minden csoport mérhető, például az aszimptomatikus, vagy látens esetek sem. Ám ahhoz, hogy a modellt használhassuk, ezek valamilyen fokú ismeretére is szükség van. A kórházban ápoltak, vagy elhunytak száma viszont jól mérhető” – hívta fel a figyelmet a szakértő, ezért első lépésként ún. állapotbecslőt terveztek, amely a mérhető állapotok és a jelen időpontig alkalmazott kontrollstratégia alapján becslést ad a többi állapotváltozó aktuális értékére. „Ez azért fontos, mert az általunk megalkotott szabályozás ún. teljes állapotvisszacsatolást valósít meg, azaz az irányítás megtervezéséhez szükség van az összes állapotváltozó ismeretére. Az állapotbecslő bizonytalan modellparaméterek esetén is megbízhatóan működött” – jelentette ki Péni Tamás, így a kutatók erre alapozva kezdték meg a prediktív irányítási stratégia megtervezését a modellre, miszerint: a rendszer pillanatnyi állapotát, a járvány dinamikáját, a betegcsoportokat ismerve egy adott horizonton előrejelzés adható arra, hogy a járvány miképpen alakulhat a különböző beavatkozások függvényében.

„A matematikai előrejelzést felhasználva egy numerikus optimalizálási eljárással meg tudjuk tervezni az optimális beavatkozó jelet, és ezen belül figyelembe tudjuk venni a megfelelő szigorú korlátozásokat és követelményeket, ilyen lehet például, hogy a kórházban ápoltak száma 10.000 alatt maradjon. Sok különböző tényező – például a kontaktusok számának csökkentése, a távolságtartás vagy a maszkviselés – besűríthető volt egyetlen, 0 és 1 közötti paraméterbe: a 0 érték felel meg annak az esetnek, amikor nem avatkozunk be a járvány terjedésébe. Ahogy az érték közeledik az 1-hez, egyre szigorúbb intézkedések bevezetését jelenti. Forgatókönyveket írtunk a különböző mértékű beavatkozó jelek hatására és ezeket vizsgálva publikáltuk az eredményeket” – részletezte a szakember. A két érték két különböző stratégiaalkotási elvnek is az alapját képezi. A mérséklésen alapuló stratégia lényege, hogy csak olyan megszorító intézkedéseket hoznak, amelyek a kórházi kapacitásokon nem nőnek túl, egyúttal a társadalom oldalán jelentkező költségek lefaragását segíthetik. Az elfojtásnál pedig a járvány elején nagyon szigorú intézkedések jönnek, amelyeket később fokozatosan enyhítenek. Ekkor korai szakaszában megállítható a terjedés: sok országhoz hasonlóan Magyarország is az utóbbit választotta a tavaszi hullám idején.

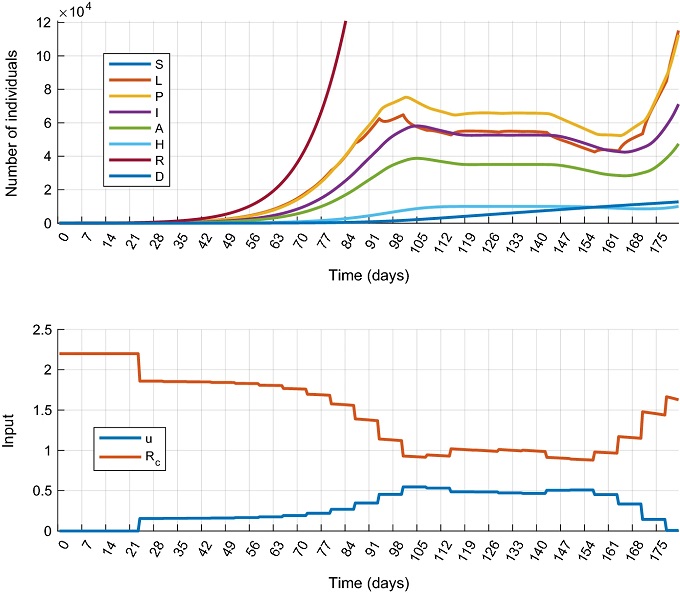
A mérséklésre alapuló forgatókönyv szimulációs eredményei. A felső grafikonon a népesség különféle csoportjainak járványgörbéje látható (S: lehetséges fertőzöttek, L: látens hordozók, P: preszimptomatikus hordozók, A: aszimptomatikus hordozók, I: fertőzöttek, R: gyógyultak, D: elhunytak)

Az alsó grafikon az „u” beavatkozó jel (azaz milyen szigorú intézkedések történtek) valamint a vírus reprodukciós rátája (Rc) közötti összefüggést mutatja az idő függvényében. A 22 napot követő intézkedések eredményeképpen csökkent a fertőzőképesség, majd hónapokkal később – az intézkedések gyengülésével – újra növekedésnek indult.

A kutatók munkájának eredményeképpen elkészült egy szoftver, ami a fél éves időszak járványkezelő stratégiáját modellezi, és megmutatja, hogy a különböző erősségű beavatkozásoknak milyen eredménye lehet. A program által generált járványgörbe értékeinek vizsgálata segítheti a döntéshozókat a tervezésben, előrejelzésben. Az irányítás fontos jellemzője, hogy periodikusan újraszámolható értékekkel dolgozzon: a kutatók egyhetes időszakot állítottak be, mert az intézkedések hatásának kifejtéséhez idő kell, egy-egy napra nincs értelme számolni, tervezni.

Péni Tamás elmondta, a SZTAKI laboratóriuma a BME Közlekedés- és Járműirányítási Tanszékkel intézményi kiválósági program keretében hosszú évek óta szoros együttműködésben közös kutatásokat végez. „Főként a gépi tanulásra, mesterséges intelligenciára, optimalizálásra épülő korszerű irányítási algoritmusok kidolgozásával foglalkozunk, természetesen közlekedési rendszerekre, autonóm járművekre is fókuszálva. Egy autonóm drón pályakövetésére, akadályelkerülésére is az optimalizálás alapú prediktív irányítási stratégiákat használjuk, így – a járványterjedés modelljének nyilvánvaló különbségei ellenére – össze tudtak kapcsolódni ezek a technikák” – számolt be a szabályozáselméleti szakértő az izgalmas közös munkáról. Megerősítette: tovább dolgoznak, hiszen a modellt a vakcinát még nem alkalmazó állapothoz igazították, ám kollégái már foglalkoznak a stratégia újragondolásával az oltások megkezdését követő periódusra. „Sokat tanultunk az elmúlt időszakból: óvatosnak kell lennünk, mert ha le is küzdjük a mostani pandémiát, számolni kell azzal, hogy megjelenhetnek hasonló, vagy akár még veszélyesebb fertőzések is. Érdemes megtartani és fejleszteni az elemzéshez használt és bevált matematikai módszereket és készülni a jövőre” – összegezte a kutató.

HA-TZS

Fotó: Takács Ildikó