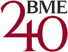Neves műegyetemi matematikusok korszakalkotó eredményeiről hallhattunk érdekességeket a BME Science Campus tudománynépszerűsítő előadásán.

„Nemcsak a tudományos világ, hanem a mai fiatalok előtt is példaként szolgálhat a munkássága annak a műegyetemi professzornak, akit a fiataloknak mutattam be előadásomban. Kőnig Dénes (1884-1944) nemcsak a BME-n, hanem a világon is elsőként tartott önálló egyetemi kurzust a gráfelméletről, emellett ő a szerzője a világ első gráfelméletről szóló könyvének is. A professzor iskolateremtő hatása, jelentős tudománynépszerűsítő tevékenysége máig érezhető a magyar matematikában, eredményei alapvető fontosságúak a gráfelméletben, több tétele a matematikai, a villamosmérnöki, valamint a mérnök-informatikai alapképzés fontos részét képezi” – mutatta be a Science Campus programsorozat keretében tartott ismeretterjesztő előadásának tartalmát Recski András, a BME Villamosmérnöki és Informatikai Kar (BME VIK) Számítástudományi és Információelméleti Tanszékének egyetemi tanára.

Az előadás résztvevői a természettudományi ismeretek mellett a Műegyetem történelmébe is betekintést kaptak. Recski András felelevenítette a 18. század végi földméréssel, vízgazdálkodással kapcsolatos szakemberigényt, amit az egyetem egykori neve (Institutum Geometrico-Hydrotechnicum) is reprezentált. Kőnig Dénes egyik legkiemelkedőbb eredménye az ún. hozzárendelési probléma gyors és hatékony megoldására adott algoritmusa. Recski András ezen elmélet magyarázatára gyakorlati példát is hozott: „egy műhelyben szét kell osztani a dolgozók között az elvégzendő, egy személyes és egy napos feladatokat úgy, hogy nem minden munkás képes tetszőleges feladat elvégzésére. Tegyük fel, hogy 5 feladatot szükséges felosztani 6 munkás között úgy, hogy az első munkás csak az első két feladathoz, a második csak az első három feladathoz ért, …, míg a hatodik dolgozó csak a harmadik és a negyedik feladatot tudja elvégezni. Ekkor a pontos helyzetet a lenti ábrán látható ún. páros gráf szemlélteti” – magyarázta Recski András: a feladatok és a munkások az „A” és a „B” halmazok pontjai, a köztük lévő élek pedig az egyes feladatokhoz kapcsolódó szakértelmeket jelzik. A feladat egy lehetséges megoldását a vastag, piros vonalak szemléltetik. „Általánosan fogalmazva, „a” mennyiségű feladat és „b” számú dolgozó esetén az összes lehetőségek száma elvileg akár b X (b–1) X … X (b–a+1) is lehetne. Ezek gépies végigpróbálása még a leggyorsabb számítógépeknek is évmilliókig tartana, ha „a” és „b” kellően nagy, legalább 60-80 körüli érték. Kőnig Dénes a problémára egy olyan algoritmust alkotott meg, amelyet egy átlagos számítógép is gyorsan végrehajt még akkor is, ha „a” és „b” értéke akár több ezer” – osztotta meg a fiatalokkal is ezt az eredményt a VIK oktatója.

Páros gráf szemléltetése

(Forrás: Szeszlér Dávid: Bevezetés a számításelméletbe 2, egyetemi jegyzet, BME VIK SzIT, 2021.)

Kőnig Dénes professzor munkássága többeket inspirált: köztük tanítványát, Gallai Tibort, (1912-1992) akinek egyes gráfelméleti eredményeit a BME-n jelenleg is zajló diszkrét matematikai kutatásoknál is alkalmazzák. Gallai algoritmusa az informatikai és villamosmérnöki ipari alkalmazásokat is segíti: egyik tételét például integrált áramköri chip-ek tervezésénél, a többrétegű huzalozásnál is alkalmazzák. Mellette Kőnig Dénes olyan neves matematikusokat is inspirált, mint Erdős Pál, Klein Eszter, Szekeres György vagy Turán Pál, akiknek későbbi munkásságában a gráfelmélet és a diszkrét matematika is jelentős szerepet kapott. Ez a terület egyébként a nemzetközi berkekben is nagyra tartott magyar matematika egyik legsikeresebb ága, többek között a nemrégiben Abel-díjat nyert Szemerédi Endre és Lovász László legfontosabb kutatási eredményei is ide sorolhatók.

„A matematikán belül a diszkrét matematika az egyik legalkalmasabb részterület arra, hogy már középiskolás korban ismertessük pályaválasztás előtt állókkal a matematika, a természettudományok szépségét, és a felfedezések örömét” – érvelt témaválasztása mellett Recski András, aki oktatóként fontosnak tartja, hogy a diákok, sőt, a szélesebb magyar közvélemény is tisztában legyen a hazai mérnöki, műszaki és természettudományi eredményekkel, a sikereket elérő szakemberekkel, akik valódi értékek létrehozásával öregbítették hazánk hírnevét.

A Science Campus előadáson résztvevő fiatalok megtudhatták azt is, hogy a BME VIK Számítástudományi és Információelméleti Tanszék szorosan együttműködik az Eötvös Loránd Tudományegyetem (ELTE) Természettudományi Kara Operációkutatás Tanszékével: közösen kezdeményezték például azt, hogy a diszkrét matematikával foglalkozó kutatók, PhD-hallgatók folyamatos szakmai kapcsolatban legyenek és személyesen is találkozzanak japán matematikusokkal. 1999 óta minden második évben a BME és az ELTE részvételével rendezik meg a japán-magyar diszkrét matematikai, kombinatorikai konferenciákat, felváltva japán és magyar helyszínekkel. 2022-ben a szervezők tervezetten már a 12. ilyen szakmai eseményt hívják életre, ahol lehetőség nyílik a diszkrét matematika elméleti megállapításait és alkalmazási lehetőségeit közelíteni, továbbá kiváló szakmai fórum a matematikai és műszaki határterületek találkozására, a műszaki gyakorlati lehetőségek iránt érdeklődő matematikusok és a matematikát intenzíven alkalmazó mérnökök számára.

„A matematika tudományát sokan maguktól távoli, bonyolult területnek vélik, holott mindennapjaink elemi alkotója, ami nélkül a világ nem lenne olyan, amilyennek ismerjük. A matematika számos ága megjelenik a művészetben, az irodalomban, az építészetben, a képzőművészetben, sőt, még az emberi kapcsolatokban is” – hívta fel a figyelmet Recski András, aki szerint a matematikai összefüggések megértéséhez különösen a fiatalok számára fontos a játékosság, a szemléltető eszközök és az egyszerű, nem elrugaszkodott magyarázatok. A Science Campus tudományos, ismeretterjesztő előadásain erre nyílik lehetősége az érdeklődőknek.

TZS-HA

Fotók forrása: Recski András előadásának részletei