2021. december 06.
Rangos nemzetközi matematikai díjjal jutalmazták Pach Péter Pált a kombinatorikai kutatásokkal foglalkozó tudományos munkájáért.
 |
„Megtiszteltetés számomra, hogy munkámat, kutatásaimat a matematika tudományának ezen elismerésére vélték érdemesnek. A díjat korábban számos kiváló matematikus nyerte el” – nyilatkozta a bme.hu-nak Pach Péter Pál, a BME Villamosmérnöki és Informatikai Kar (VIK) Számítástudományi és Információelméleti Tanszékének egyetemi docense, az MTA-BME Lendület Aritmetikai Kombinatorika Kutatócsoport alapítója és vezetője, aki rangos nemzetközi kitüntetésben részesült a diszkrét matematika, ezen belül a kombinatorikus algebra, a részben rendezett halmazok és a kombinatorikus számelmélet terén végzett tudományos munkája elismeréseként. |
|
A „European Prize in Combinatorics” nevű díjat a kombinatorika, a diszkrét matematika és ezek alkalmazásai terén elért kiemelkedő eredményekért fiatal, 35 év alatti európai kutatóknak ítélik oda. Az elismerést 2003-ban osztották ki először, azóta kétévente lel gazdára a rangos szakmai kitüntetés, melyet a EuroComb konferencián, a kombinatorika, a gráfelmélet és ezek lehetséges felhasználásával foglalkozó európai szakmai platformon adnak át. A 2500 euró pénzjutalommal járó díjat a matematika tudományának élvonalába tartozó kutatók nyerték már el a világ különböző kiváló felsőoktatási intézményeiből. A magyar matematikai, ezen belül a kombinatorikai iskola világviszonylatban is kiemelkedőnek számít, az eddigi 22 díjazott között immár három magyar matematikus is található. 2021-ben 4 matematikust ismert el a pályázatokat elbíráló zsűri az alábbi indoklással: Pach Péter Pál, a BME kutatója, a diszkrét matematikában, különösen a kombinatorikus algebra, a részben rendezett halmazok és a kombinatorikus számelmélet terén elért számos mély eredményéért. Croottal és Levvel közös tétele (Z_4)^n számtani sorozatot nem tartalmazó részhalmazairól mérföldkőnek számít a diszkrét matematikában. Julian Sahasrabudhe, a University of Cambridge kutatója, aki mély és fontos eredményeket igazolt kombinatorikus módszereket alkalmazva a harmonikus analízis, a kombinatorikus számelmélet, a Ramsey-elmélet és a valószínűségszámítás területén. Speciálisan, frappáns megoldásokat adott Littlewood problémáira, a polinomok geometriájára, továbbá Erdős, Schinzel és Selfridge 50 éves kérdéseire. Lisa Sauermann, a Massachusetts Institute of Technology (MIT) kutatója, a kombinatorika területén elért mély eredményeiért, speciálisan algebrailag definiált osztályok növekedéséről szóló eredményéért, Erdős, Faudree, Rousseau és Schelp kérdéséninek megválaszolásáért és az élstatisztika sejtés megoldásáért. Tomon István, a zürichi ETH (Eidgenössische Technische Hochschule) kutatója, az extremális kombinatorika és a részben rendezett halmazok elmélete terén elért alapvető eredményeiért. Speciálisan, az Erdős-Hajnal sejtés megoldásáért string gráfokra, továbbá Brown, Erdős és Sós egy felületek extremális számára vonatkozó problémájának megoldásáért. |
A műegyetemi oktató-kutató tudományos munkája az aritmetikai kombinatorika területéhez tartozik. Itt olyan kombinatorikus kérdéseket vizsgálnak, ahol fontos szerepet kap valamilyen aritmetikai struktúra is. Pach Péter Pál gyakran alkalmaz olyan algebrai módszereket, mint például a „polinom módszer” és ennek különböző változatait. Szemléltető példa egy központi vizsgált kérdésre: egy véges test feletti vektortérben legfeljebb hány pont választható ki úgy, hogy semelyik három (vagy általánosabban, semelyik k) ne alkosson számtani sorozatot? A kérdés motivációja egyrészt véges geometriai, ugyanis három számtani sorozatot alkotó pont szükségképpen egy egyenesre esik, és az olyan halmazok méretének vizsgálata, melyek semelyik egyenesnek nem tartalmazzák 2-nél több pontját – az ilyen tulajdonságú halmazokat cap-eknek nevezzük – sokat vizsgált kérdés. Másrészt annak a számelméleti problémának is egy gyakran használt modellje, hogy az 1, 2, ..., n számok közül hány választható ki úgy, hogy semelyik három (vagy általánosabban, semelyik k) ne alkosson számtani sorozatot. Szemerédi Endre Abel-díjas matematikus híres eredménye szerint az 1, 2, ..., n számok egy rögzített, pozitív sűrűségű részét kiválasztva mindenképpen létrejön k hosszú számtani sorozat (ha n elegendően nagy). A kérdés véges testek feletti változatában (is) sokáig Fourier-analízist használva igazoltak egyre erősebb eredményeket, ám Pach Péter Pál és szerzőtársai, Croot és Lev kifejlesztették a polinom módszer egy új változatát, amelynek segítségével nem csak ennél a kérdésnél, hanem számos másiknál is áttörést sikerült elérni.

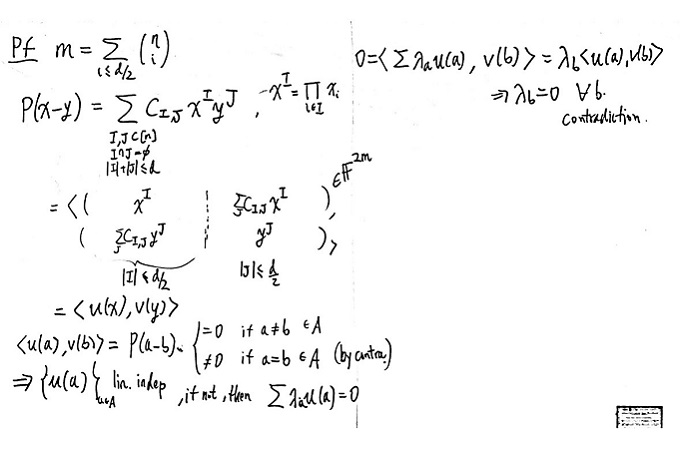
Pach Péter Pál és szerzőtársai, Croot és Lev által kifejlesztett polinom módszer új változatát a közzététel után 5 nappal már Oxfordban oktatták (részlet Yufei Zhao 2016. május 10-i előadásából – forrás)
|
Timothy Gowers Fields-érmes matematikus a következőképpen írt blogján Pach Péter Pál és szerzőtársai, Croot és Lev által kifejlesztett polinom módszer új változatáról. Véleménye angol nyelven: „From time to time an argument comes along that appears to present a stiff challenge to my view. The solution to the cap-set problem is a very good example: it’s easy to understand the proof, but the argument has a magic quality that leaves one wondering how on earth anybody thought of it. I’m referring particularly to the Croot-Lev-Pach lemma here.” |
Pach Péter Pál és kutatócsoportja úgy nevezett Ramsey-típusú kérdéseket is vizsgál. A Ramsey-elméletben valamilyen alaphalmazt több színnel színezve keresünk bizonyos konfigurációt, melyet egyformára színeztek. Green és Lindqvist egyik eredménye szerint a pozitív egész számokat akárhogyan is színezzük két színnel, biztosan lesznek olyan egymástól különböző, egyformán színezett x, y és z számok, melyekre x+y=z2. Ezt úgy is mondhatjuk, hogy az egyenletnek létrejön monokromatikus megoldása. Pach Péter Pál erre egy másik bizonyítást adott, melyre építve Hong Liuval és a Lendület kutatócsoport egy másik tagjával, Sándor Csabával (tanszékvezető-helyettes egyetemi docens, TTK Matematika Intézet, Sztochasztika Tanszék, és Bolyai-plakettet nyert műegyetemi matematikus) kiterjesztették arra az esetre, amikor z2 helyett tetszőleges fokszámú polinom állhat az egyenlet jobb oldalán.
Pach Péter Pál korábban elnyerte a Bolyai János Kutatási Ösztöndíjat (az ösztöndíjas időszakban elért eredményeiért Bolyai-plakettet kapott), az Erdős Pál Fiatal Kutatói Ösztöndíjat, majd 2019-ben a Magyar Tudományos Akadémia Lendület programjában is támogatást nyert, és így az ugyanekkor elnyert MTA Prémium posztdoktori ösztöndíjtól visszalépett. Ekkor megalapította a MTA-BME Lendület Aritmetikai Kombinatorika Kutatócsoportot, amely a közelmúltban komoly eredményt ért el: Pach Péter Pál és kutatótársa, Nagy János igazolta Alon-Jaeger-Tarsi 1981-es sejtését. E szerint invertálható „A” mátrix esetén mindig található olyan x vektor, melyre sem x-nek, sem Ax-nek nincs 0 koordinátája. Másképpen megfogalmazva: akárhogyan is veszünk két „koordinátarendszert”, lesz olyan vektor, amelyiknek egyikben sincs 0 koordinátája. A sejtés véges testek felett érdekes, ezen belül is a prímtestek esetén volt nyitott. 2021 nyarán azt sikerült igazolniuk, hogy a sejtés teljesül abban az esetben, ha a test elemszáma elegendően nagy (legalább 80). A kérdés 3 csillagos besorolású az „Open Problems Gardenben”.
.Ősszel immáron Tomon Istvánnal közösen, a kidolgozott módszert továbbfejlesztve, és annak újabb alkalmazásaként előrelépést sikerült elérniük az additív bázis sejtésben, illetve csoportok részcsoportokkal való fedésével kapcsolat problémákban is.
Pach Péter Pál elméleti matematikai kutatásokkal foglalkozik. E kutatásokban a vizsgálandó kérdéseket, megoldandó problémákat elsősorban a matematika „belső logikája”, a kérdések szépsége és nehézsége alapján választják ki. A kutatómunka legizgalmasabb része új összefüggések keresése, már létező módszerek továbbfejlesztése újabb ötletekkel. Sok elméleti kutatót, így Pach Péter Pált is ez az intellektuális kihívás inspirálja, és a felfedezés öröme motiválja. Fontos megemlíteni, hogy bár a kérdések a matematikán belülről érkeznek, gyakran néhány állomással később, akár már a hétköznapokban hasznosulva is visszaköszönhetnek az elért eredmények. Különösen igaz ez a kombinatorikára, ami a számítástudományon és az információelméleten keresztül már a mindennapi életben is hasznosítható alkalmazásokhoz járulhat hozzá. Például Pach Péter Pál és kutatótársainak fentebb említett, számtani sorozatokkal kapcsolatos eredményei, az itt kidolgozott módszerük a mátrixszorzás lépésszámának gyorsításával kapcsolatos kutatásokban is hasznosult. A vizsgált kérdések egy részének információelméleti vonatkozása is van, ami szintén egy olyan terület, aminek eredményeit a mindennapjainkban is hasznosítjuk.
„A zsűri elnöke, Jaroslav Nešetřil leveléből értesültem arról, hogy idén engem is a díjazottak közé választottak. A pandémiás helyzet miatt online rendezték meg a barcelonai EuroComb konferenciát, amelynek keretében átadták az elismerést. A díjazottak ’prize lecture-t’ tartottak, azaz a díj ’átvétele’ után bemutatták kutatásukat a konferencián” – ecsetelte a műegyetemi kutató, akit a jövőbeli terveiről is kérdeztünk. „A jövőmet továbbra is döntően itthon képzelem el. Fél-egy éves külföldi vendégkutatói időszak lehetőségével is számolok valamikor a következő 5-10 év során, ezt a saját szempontjaim-lehetőségeim mellett persze a feleségem munkája és három gyermekünk tanulmányai is befolyásolják” – zárta gondolatait Pach Péter Pál.
TZS-HA
Fotók forrása: Pach Péter Pál